[A:5v]

9^a Si conus plano secetur coincidente ad alterum latus trianguli per axim neque penes¹¹¹ basim ducto, neque subcontrarie posito; facta sectio non erit circulus .

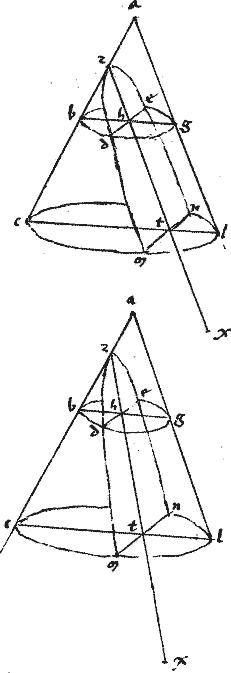
Conus, cuius vertex a basis autem circulus bg secetur plano quodam, quod neque basi aequidistans, neque subcontrarium sit: et faciat in superficie sectionem dce.

Dico quod dce periferia¹¹² non est circulus.

Sit enim si possibile est, et coincidat planum basi: sitque communis sectio zh centrum basis t a quo cathetus ducatur ab zh quae sit th. Et producatur per ht et axim¹¹³ planum faciens, per 3^am huius, in superficie triangulum abg cuius cum plano dce sectio sit recta dhe. Et a puncto quopiam periferiae dce quod sit c ducatur cml aequidistans ipsi zh eritque, per antepremissam cm aequalis ipsi ml quare de diameter est circuli de cum ipsa el et omnes similiter ei parallelum¹¹⁴ bifariam secet. Itaque sit nmx aequidistans ipsi bg et quoniam cl ipsi zh aequidistat: iam per 15^am 11ⁱ Euclidis planum, in quo nx cm ipsi circulo bzg ¹¹⁵ aequedistabit: facietque, per 4^am , in superficie coni circulum ncx. Et quoniam zh est ad rectos bh et ipsa quoque cm per 10^am 11ⁱ Euclidis ad rectos erit ipsi nx.

Quamobrem per 34^am 3ⁱⁱ Euclidis nm mx aequum est cm scilicet per eamdem cm aequum est dm me cum ncx circulus sit: et dce circulus supponatur et ideo dm me aequale ^lo nm mx. Igitur per 15^am 6ⁱ¹¹⁶ Euclidis sicut nm md sic me mx cumque dmn¹¹⁷ emx angulos ad m per 15^am primi Euclidis habeant aequales ; iam per per 6^am sexti, aequiangula erunt ad invicem: itaque anguli dnm mex proportionalibus lateribus oppositi sunt invicem aequales. Verum anguli dnm abg aequales, propter aequidistantiam linearum nx bg. Igitur anguli abg mex aequales. Et perinde sectio subcontraria est: quod est contra hypothesim. Non est ergo circulus sectio dce et hoc fuit demonstrandum.