F  r  a  n  c  i  s  c  i        M  a  u  r  o  l  y  c  i        O  p  e  r  a        M  a  t  h  e  m  a  t  i  c  a
Introduzione Help Pianta Sommario
Archimedis liber de sphaera et cylindro 22
<- App. -> <- = ->

PROPOSITIO XXII.

Conus, cuius celsitudo aequalis est aggregato celsitudinum quotlibet conorum super aequas bases est aequalis aggregato illorum.

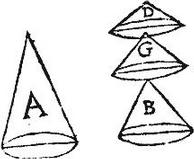
figura 26

Exempli causa, celsitudo coni A sit aequalis celsitudinibus aliquot conorum ut puta trium B, G, D: sintque omnium bases aequales. Aio quod conus A aequalis est conis B, G, D simul sumptis: nam cum eorum bases sint aequales, erit per 11.12. conus B ad conum A, sicut altitudo coni B ad altitudinem coni A: item conus G ad conum A, sicut altitudo coni G ad altitudinem coni A: ergo per 24.5. coni B, G, simul ad conum A, sicut altitudines conorum B, G, simul sumptae ad conum A: adhuc conus D ad conum A, sicut altitudo coni D ad altitudinem coni A. Rursum ergo per 24.5. coni B, G, D, simul ad conum A, sicut altitudines conorum B, G, D, simul sumptae ad coni A celsitudinem: sed celsitudines conorum B, G, D, simul sumptae aequales sunt celsitudini coni A: ergo et coni B, G, D, simul sumpti aequales sunt cono A: quod est propositum. Idem de quotcumque conis demonstrabimus repetita quoties opus fuerit 24.5. quod propositum est.

Inizio della pagina
 ->