Chiacchierata sulla teoria algoritmica dell'informazione

Ho deciso di scrivere questa nota introduttiva alla teoriaalgoritmica dell' informazione nella forma di dialogo per almeno tre motivi.

Il primo è per renderla più agevole e divertente ad un lettoreche potrebbe venire scoraggiato da un articolo scritto in modo sistematico:con la forma del dialogo si susseguono domande e risposte e quindi diventapiù facile seguire il filo logico.

Il secondo motivo nasce dal fatto che io non sono un esperto diquesta teoria. Mettendo le varie affermazioni nelle bocche dei signori A. eB., posso tranquillamente dissociarmi dalle loro affermazioni qualora sidovessero rivelare esposte in modo approssimativo ed un po' impreciso.

La terza motivazione sta nel fatto che questi due signori sonogiovani studenti ed in quanto tali hanno tutto il diritto di fare galopparela loro fantasia, diritto che non si addice a un professore. Noi tutti siamodisposti a perdonare le loro estrapolazioni anche quando sono un po' troppoardite, ma un professore deve essere una persona seria (anche quando diventanoioso).

Naturalmente esiste anche il rovescio della medaglia: questi duesignori non sempre si esprimono in buon italiano. Mescolano vocabolitecnico-scientifici con parole del gergo studentesco e qualche volta usanovocaboli troppo coloriti che fanno disonore al mondo accademico: ma ancheall'Università se ne vedono di tutti i colori e bisogna rassegnarsi.

A.- Però si incontrano persone interessanti e si parla di molte cose,anche fuori dei corsi ufficiali. Per esempio, parlando con alcuni compagni econ i professori ho scoperto una teoria molto interessante che rispondeanche ad alcune questioni filosofiche che ti dovrebbero interessare.

A.- Sì, il nome è complicato ma i fondamenti della teoria sonoabbastanza semplici.

$\begin{displaymath}%% S_1=''0001000100010001000100010001000100010001'' %% \end{displaymath}$

$\begin{displaymath}%% S_2=''1110010111001101101011010011001111101101''. %% \end{displaymath}$

A.- Non fare lo spiritoso ed il purista della lingua italiana; sai bene cheoggi si usa la parola ''stringa'' per denotare una successione finita di 0 edi 1. Ammetto che è una brutta traduzione della parola inglese string ma con tutti questi computer che girano, ormai èentrata a fare parte della lingua parlata.

Dopo avere osservato per pochi secondi queste due stringhe il signorB da la sua risposta.

B.- Mi sembra che la tua domanda sia demenziale, è ovvio che la stringacasuale è la

A.- Se la mia domanda è demenziale, lo è di più la tua rispostaperchè non mi hai dato alcuna motivazione.

B.- E' ovvio che la prima stringa non è casuale perchè segue una regola ben precisa: è formata da tre ''0'' ed un ''1'' che si ripetonoper dieci volte.

A.- Ma anche la seconda stringa potrebbe avere una regola nascosta.Per esempio si potrebbe ottenere con la seguente regola

$\begin{eqnarray*}%% &&\mbox{prendi il decimo numero primo}, \\ %% &&\mbox{sommac... ...zione binaria,} \\ %% &&\mbox{e cos\\lq \i\ otterrai la stringa }S_2\end{eqnarray*}$

A.- Neanche io, ma posso sostenere senz'altro che la stringa

seguecertamente qualche regola nascosta, perchè essendoci infinite regole, essapuò senz'altro essere ottenuta mediante alcune di esse.

B.- Questo è certamente vero, ma la

segue una regola semplice e conquesto ti ho fregato.

A.- Bravo! Hai fatto centro...basta che tu mi definisca quando una regola sidice semplice.

A.-E chi ti dice che la

non segua una regola che io ho capito subitoquando l'ho scritta.

A.- In questo modo hai semplicemente cambiato nome ai termini del problema.Hai sostituito la parola complessità alla parola casualità. Possiamo convenire che la casualità e la complessità sono due concetti strettamente collegati ma non hai rispostoalla mia domanda iniziale. Se ti fa piacere a questo punto ti riformula lata domanda con i termini che preferisci:

Il signor B rimane un po' interdetto e si mette a riflettere; alloral'amico riprende la parola.

A.- Ti voglio aiutare. Una di queste stringhe l'ho prodotta con questamoneta. L'ho lanciata in aria per 40 volte ed ho scritto un ''1'' quando miè venuto testa ed uno ''0'' quando mi è venuto croce. Questainformazione ti aiuta? Sai dirmi quale delle due stringhe

èstata prodotta col metodo del lancio di una moneta?

B.- Perchè per ottenere una stringa come la

avresti dovuto passarequalche secolo a lanciare monete.

A.- Ammetto che la

è stata prodotta col metodo del lancio di unamoneta, ma tu non mi hai ancora risposto alla domanda iniziale.

B.- Adesso la risposta è semplice; la stringa casuale è la seconda,perchè è stata prodotta con un metodo casuale, cioè il lancio dellatua moneta.

A.- Veramente tu hai risposto ad un'altra domanda: quale delle due stringheè stata prodotta casualmente, non quale è casuale.

A.- Non è vero infatti non lo potrai mai provare. Lancia questa moneta evediamo se ti viene la stringa

B.- Non fare lo spiritoso, sai che questo è impossibile; ognuna di questedue stringhe ha la stessa probabilità di uscire che è 2 $^{-40}.$

A.- Da questo punto di vista le due stringhe sono equivalenti. Ognuna diesse ha la probabilità di essere prodotta con lanci casuali di uno su 1trilione e 99 miliardi 511 milioni 627 mila 776.

A.- Non divagare. Tu non hai ancora risposto alla mia domanda per almeno duemotivi: io voglio sapere se una delle due stringhe possa ritenersi casualein se stessa e non per il modo in cui è stata prodotta; inoltre se tu usinozioni probabilistiche devi spiegarmi cosa intendi per probabilità.

B.- Ma sai bene che la probabilità è un concetto essenzialmenteindefinibile. Hanno versato fiumi di inchiostro per definire laprobabilità ed ogni definizione di probabilità (frequentista,soggettivista etc.) si è sempre prestata ad un mare di obiezioni.

A.- E' proprio qui che ti volevo. Se tu definisci quale delle due stringheè casuale in un certo senso definisci cos'è il caso, ovvero ilfondamento della nozione di probabilità.

A.- Prendiamo nuovamente questa moneta. Tu dici che la probabilità cheesca testa o croce è esattamente 1/2. Questo perchè 1/2 è l'inversodel numero degli eventi possibili purchè questi eventi siano equiprobabili.

B.- E questa è una definizione circolare in quanto usi il concetto di equi-probabilità per definire la probabiltà.

A.- Proprio così. Quindi dobbiamo avere un criterio per sapere se leuscite di testa o croce di questa moneta sono equiprobabili. Che cosadiresti se lanciando questa moneta ottenessi la stringa

A.- Dunque, per sapere se la mia moneta è un oggetto i cui lanci sicomportano in maniera casuale devo sapere che cosa è una stringa casuale.

B.- In pratica questo va bene, ma dal punto di vista astratto no; infatti daun punto di vista puramente teorico, non si può escludere che la stringa

sia stata ottenuta col lancio della moneta.

A.- Hai ragione, ma solo in parte. Infatti la stringa

ha una qualcheprobabilità di essere prodotta a caso solo perchè è molto corta. Bastache tu la prenda un po' più lunga e la probabilità diventeràpraticamente 0. Per esempio, producendo una stringa al secondo, per ottenereuna data stringa di 60 caratteri, non basta l'età dell'universo.

B.- Va bene, ma dal punto di vista teorico, tra 2 $^{-40}$ e 2 $^{-60}$ noncambia nulla.

A.- Ma non essere sciocco. Io so rispondere a tutte le tue domande perchèsono un personaggio inventato dall'Autore proprio con questo scopo. Perevitare il problema che tu dici basta prendere stringhe casuali infinite esviluppare il calcolo delle probabiltà come ha fatto Von Mises più di 50anni fa.

A.- No, perchè Von Mises ha basato la nozione di probabiltà su quella disuccessione casuale, ma non è riuscito a dare una buona nozione di stringacasuale. Con questa teoria invece si può definire che cos'è unasuccessione casuale: basta che ogni segmento iniziale della successione siauna stringa casuale.....

B.- Va bene! Ti do atto che tu sai tutto, ma smettila di usare parole troppodifficili perchè tanto non ci capisco nulla.

A.- Bene. Allora ragioniamo più alla buona. Se io ti mostro le stringhe

e $S_2\;$ e ti dico che una di esse è stata prodotta a caso mi diciche questa stringa è la

ma non sai il perchè.

B.- Questo è vero, ma solo perchè non ho studiato statistica.Altrimenti, potrei applicare uno dei molti test statistici e darti unarisposta definitiva.

A.- Anche questo non è vero. Tu sai che un computer $\,$ qualsiasi, anche con un programmino molto semplice, riesce a produrrestringhe casuali che resistono alla maggior parte dei test statistici. Maqueste stringhe non sono casuali perchè sono prodotte da un programmadetermistico, infatti vengono chiamate stringhe (o successioni) pseudocasuali.

B.- Ma almeno in linea di principio si può ammettere l'esistenza di teststatistici che smascherino tutte le stringhe pseudocasuali.

A.-Certo, ma per fare una distinzione appropriata tra stringhe casuali epseudocasuali devi avere già definito che cosa intendi per stringhecasuali, altrimenti come fai a smascherare le pseudocasuali?

A.- A questo punto della nostra discussione abbiamo appurato che ricorrere anozioni probabilistiche per rispondere alla domanda iniziale non aiutaaffatto, perchè per dare una definizione non assiomatica di probabilitàdevi già sapere che cos'è una stringa casuale per distinguerla da unapseudocasuale. Quindi devi definire la casualità in maniera intrinseca. Seriesci a fare ciò, non solo sai che cos'è una stringa casuale, ma dai unfondamento accettabile al calcolo delle probabilità.

B.- Nessuna stringa è casuale. Tutto segue una regola. Ciò che esiste,esiste per necessità. Come dice Hegel ciò che è reale è razionale.Quello che esiste, esiste per volontà di Dio e niente può esserelasciato al caso. Ciò che noi chiamiamo caso è solo la misura dellanostra ignoranza...

A.- ...e magari è frutto del demonio, una prova dell'esistenza di Satana.Non essere ridicolo, lo so che sei bravo in filosofia, ma noi vogliamo fareun discorso terra terra e non è il caso di scomodare Dio. Vogliamo saperesolo perche la

è causale e la risposta, anche se è concettualmenteprofonda, deve essere formalmente semplice.

A.-Supponi che io voglia comunicare la mia stringa ad un amico chevive...sulla luna e che le trasmissioni tra qui e la luna costino molto caree pertanto mi conviene rendere il mio messaggio il più corto possibileper risparmiare. Se voglio trasmettere la stringa $S_{1}$ basta chetrasmetta il messaggio

Per trasmettere invece la stringa $S_{2}$ non posso fare altro chetrasmettere ogni simbolo alla volta ed impiegare 20 bit.

B.- Ma devi anche trasmettere le regole per ricostruire il messaggio speditoin forma abbreviata.

A.- D'accordo, ma se parliamo di stringhe lunghe, l'informazione pertrasmettere tali regole è irrilevante.

B.- Dunque tu dici che una stringa è casuale se l'informazionenecessaria per ricostrurla è di tanti bit quanto è la lunghezzadella stringa.

B.- Aspetta un momento! Tu mi stai fregando. L'informazione necessaria pertrasmettere un messaggio dipende da quello che sa la persona che riceve ilmessaggio. Se io voglio trasmettere sulla luna il quinto canto della DivinaCommedia, non devo trasmetterlo verso per verso. Basta che trasmetta lafrase

$\begin{displaymath}%% \mbox{Il V canto della divina Commedia} %% \end{displaymath}$

B.- Quanto poco; adesso sei tu che usi concetti non non definiti e fai unagran confusione per risolvere una questione che appare evidente a priori.

A.- E' vero; in realtà molte volte questi concetti non sono insegnatineppure all'Università.

Il signor A. mostra all'amico un disegno di una macchina di Turingche appare come una scatola con un quadro munito di una lancetta che segnagli stati interni; essa poggia su una finestrella nella quale scorre unnastro simile a quello degli antichi telegrafi. Accanto si vede una tabellache schematizza il funzionamento della macchina.

B.- Mamma mia, o cos'è?...un ibrido tra un macina-caffè ed il computerdi Matusalemme?!

A. - Ma no! Questo e solo un disegno schematico. Il disegno non haimportanza; nessuno ha mai costruito veramente una macchina di Turing. Sevuoi capire devi guardare solo questa tabella qui.

A.- Comunque non ha importanza perchè al posto di una macchina di Turinguniversale si può sostituire il tuo computer con un semplice linguaggio diprogrammazione.

A.- Sì, il Basic o il Pascal fa lo stesso. L'unica astrazione che deviusare consiste nel fatto di supporre che il tuo computer abbia memoriainfinita e che tu abbia la pazienza di aspettare che il programma abbiacompletato il suo ciclo (ammesso che si fermi).

B.- Ehi, un momento; io posso immaginarmi un computer con memoria infinita,ma non posso immaginare quali grandiosi programmi ci si possa far girare.

A.- Non prendermi troppo alla lettera. Dicendo che un computer ha memoriainfinita voglio semplicemente dire che ha memoria sufficiente per farcigirare un qualunque programma; e siccome non si può sapere a priori lamemoria necessaria, si deve supporre che gli si possa aggiungere un po' dimemoria tutte le volte ciò si renda necessario.

B.- Ho capito; è come quando in un compito di esame si può semprerichiedere nuovi fogli bianchi quando si sono esauriti i fogli che ci hannodato precedentemente.

A.- Hai capito benissimo. Una macchina di Turing si dice universale se può''simulare'' ogni altra macchina di Turing. I computer che noi usiamo sonomacchine di Turing universali, infatti puoi mettergli dentro il linguaggioche ti pare: Pascal, Basic, Lisp. E ciascuno di questi linguaggi puòsimulare un qualsiasi altro linguaggio.

A.- Allora supponiamo che tu ed il tuo amico sulla luna abbiate due computercon lo stesso linguaggio di programmazione. Allora se tu vuoi fare in modoche sul display del tuo amico compaia la stringa $S_{1}$ basta che tuspedisca il seguente messaggio:

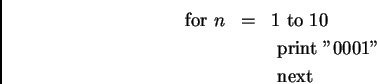
$\begin{eqnarray*}%% \mbox{for }n &=&1\mbox{ to 10} \\ %% &&\ \mbox{print ''0001''} \\ %% &&\ \mbox{next}%% \end{eqnarray*}$

$\begin{displaymath}%% \mbox{print}\;''0001000100010001000100010001000100010001''%% \end{displaymath}$

A questo punto, si può definire la quantità di informazione contenuta inuna qualunque stringa come la lunghezza del più corto programma cheproduce quella stringa.

Una volta fissata una macchina di Turing universale

, o per dirlo inparole povere, una volta fissato il linguaggio di programmazione, laquantità di informazione contenuta in una stringa

risulta essere unnumero intero ben definito. Esso sarà denotato col simbolo

$\begin{displaymath}%% I_U(x)=\min \left\{ \left\vert p\right\vert \mid U(p)=x\right\} %% \end{displaymath}$

B.- Molto semplice....ed interessante. Ma definita in questa maniera, laquantità di informazione viene a dipendere dal linguaggio diprogrammazione scelto, cioè da

A - Questo è vero; ma questa dipendenza non è troppo grave. Infatti, se

è un altro linguaggio di programmazione, risulta che

$\begin{displaymath}%% \left\vert I_U(x)-I_V(x)\right\vert \leq C(U,V) %% \end{displaymath}$

Ora, vuoi scrivere un programma che ti produce la stringa

con lamacchina

, basta che tu abbia il programma $p_{V,U}$ che permette disimulare la macchina

con la

, e poi dai alla macchina

ilprogramma $p_{U,x}$ e così otterrai la stringa

$\begin{displaymath}%% V(p_{V,U},\;p_{U,x})=x %% \end{displaymath}$

Probabilmente questa non è la maniera migliore di ottenere la stringa

dalla macchina

; quasi certamente il programma più corto $p_{V,x}$ sarà diverso dal programma $(p_{V,U},\;p_{U,x})$ ; denotando con $\left\vert%% p\right\vert$ la lunghezza di un programma si ha che

$\begin{displaymath}%% \left\vert p_{V,x}\right\vert \leq \left\vert p_{V,U}\right\vert +\left\vert p_{U,x}\right\vert %% \end{displaymath}$

$\begin{displaymath}%% \left\vert p_{V,x}\right\vert -\left\vert p_{U,x}\right\vert \leq \left\vert p_{V,U}\right\vert ; %% \end{displaymath}$

$\begin{displaymath}%% \left\vert p_{U,x}\right\vert -\left\vert p_{V,x}\right\vert \leq \left\vert p_{U,V,}\right\vert ; %% \end{displaymath}$

$\begin{displaymath}%% \left\vert \left\vert p_{V,x}\right\vert -\left\vert p_{U,... ...\vert p_{V,U}\right\vert ,\left\vert p_{U,V,}\right\vert ). %% \end{displaymath}$

$\begin{displaymath}%% I_U(x)=\left\vert p_{U,x}\right\vert %% \end{displaymath}$

$\begin{displaymath}%% I_V(x)=\left\vert p_{V,x}\right\vert , %% \end{displaymath}$

$\begin{displaymath}%% C(U,V)=\max (\left\vert p_{V,U}\right\vert ,\left\vert p_{U,V,}\right\vert ) %% \end{displaymath}$

B. - E quindi la quantità di informazione contenuta in una stringa è unconcetto ben definito, a meno di una costante. In fondo è abbastanzanaturale pensare che la quantità di informazione contenuta in una stringanon è proporzionale alla sua lunghezza, ma è una cosa indipendente chein un modo o nell'altro possa essere definita rigorosamente. Però...credodi avere perso il filo del discorso; stavamo parlando di complessità e dicasualità. Adesso siamo approdati ad una nozione abbastanza diversa.

A.- Bene possiamo riepilogare tutti i passaggi: una stringa si dice casuale se non ha regole nascoste che la possano rendere più corta.Grazie alla nozione di ''macchina di Turing universale'' queste nozionipossono essere perfettamente formalizzate (a meno di costanti che non sonorilevanti dal punto di vista generale). Infatti si può definireformalmente la quantità di informazione (chiamata anche complessità nelsenso di Kolmogorov) contenuta in una stringa; a questo punto, una stringa,può essere definita casuale se il suo contenuto di informazione

èpiù o meno uguale alla lunghezza $\left\vert x\right\vert$ della stringa stessa.

B.- Ho capito; ma che cosa vuol dire ''più o meno uguale''? Questa non è certo una asserzione matematica.

A.- Certamente; bisogna dare una valutazione quantitativa. Per motivitecnici si è deciso di definire

è casuale se

$\begin{displaymath}%% I(x)\geq \left\vert x\right\vert -\log _2\left\vert x\right\vert %% \end{displaymath}$

$\begin{displaymath}%% 1.000.000-\log _21.000.000\simeq %% \end{displaymath}$

$\begin{displaymath}%% \simeq 1.000.000-19,931\simeq %% \end{displaymath}$

B.- Quindi, almeno per stringhe sufficientemente lunghe ha senso parlare distringhe intrinsecamente casuali. Ma quante sono? Immagino che siano molte.

A. - Non sono molte, ma moltissime. Calcoliamo ad esempio quante sono lestringhe casuali di lunghezza

. In totale ci sono 2

stringhe dilunghezza

. Quelle che non sono casuali possono essere prodotte dastringhe appeno un po' più corte, ovvero da stringhe di lunghezza $N-\log _2N$ . Ma le stringhe di questa lunghezza sono al più

$\begin{displaymath}%% 2^{N-\log _2N}=\frac{2^N}N %% \end{displaymath}$

$\begin{displaymath}%% 2^N-\frac{2^N}N=(1-\frac 1N)2^N. %% \end{displaymath}$

B. - Ma allora è facile avere stringhe casuali. Anche considerandostringhe di solo cento caratteri, almeno il 99% di esse sono casuali.

A. Poichè le stringhe possono essere poste in corrispondenza biunivocacon i numeri naturali secondo la seguente tabella (ordine lessicografico)

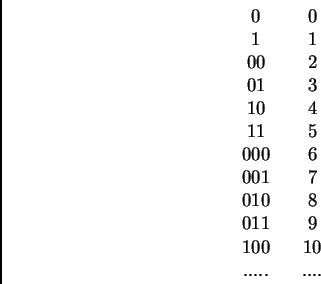
$\begin{displaymath}%% \begin{array}{ccc}%% 0 & & 0 \\ %% 1 & & 1 \\ %% 00 & & 2 ... ...11 & & 9 \\ %% 100 & & 10 \\ %% ..... & & ....%% \end{array}%% \end{displaymath}$

$\begin{displaymath}%% I(n)\geq \log _{2}(n)-\log _{2}\log _{2}(n)%% \end{displaymath}$

A. -In base alla tabella, parlare di numeri naturali o di stringhe è lastessa cosa.....

A. - .....e quindi possiamo parlare di numeri casuali. Un numero

, inbase alla tabella scritta sopra può sempre essere rappresentato con $%%% \log _{2}(n+2)$ simboli. Ma esso può anche avere delle regole nascoste;per esempio il numero

Quindi non solo ti ho spiegato cos'è una stringa casuale, ma anche cosaè un numero casuale. Naturalmente con questa definizione i numeri piccolisono tutti casuali....

B.- Senti, per le stringhe ti posso anche dare ragione, ma identificare inumeri con le stringhe e dire che in questa maniera si può definirecos'è un numero a caso mi sembra una grande forzatura. Se tu avessiragione, si avrebbe che quasi tutti i numeri sono casuali e quindi, nonpotendo distinguere un numero casuale dall'altro avrei che sono più o menoquasi tutti equiprobabili ....

A.- Io non ho detto che quasi tutti i numeri sono equiprobabili; laprobabilità a priori di un numero è un altra cosa...

B.- Non mi dire che con la tua teoria si può anche definire laprobabilità a priori di un numero o di un qualunque altro ogggetto. Tiposso dare ragione quando dici che puoi definire cos'è una stringacasuale, ma per definire la probabilità penso che ''il vecchio lanciodella moneta'' resti il metodo più efficiente, o almeno il piùintuitivo; e poichè i numeri sono infiniti, la nozione di numero casualemi sfugge.

A.- E cosa mi diresti se io affermassi che la probabilità a priori di unnumero

non è altro che

B.- Direi che è una definizione come un'altra, ma non mi sembraminimamente correlata alla idea intuitiva di probabilità che abbiamo ''apriori''. A meno che tu non abbia argomenti per convincermi.

A.- Certo che ce l'ho. Altrimenti non avrei portato in ''ballo'' questaquestione. Tu mi dici che sei ancora affezionato al vecchio buon ''lanciodella moneta''. Bene supponiamo di avere la tua moneta perfetta, lanciamolae vediamo qual'è la probabilità che mi dia un certo numero.

B.- Se tu codifichi i primi 2 $^{30}$ numeri in un qualunque modo e faitrenta lanci, è chiaro che ogni numero ha la stessa probabilità che è 2 $^{-30}.$ E ciò resta vero anche se sostituisci la moneta con una stringacasuale di 30 caratteri.

A.- Ma non correre, io non voglio fare trenta lanci, voglio fare infinitilanci. O meglio voglio fare

lanci e tenere conto di tutte le possibiltà che esistono qualunque sia il numero

B. - Forse sto capendo....Fammi indovinare: guardando la tua tabella sipuò dire che il numero 0 e il numero 1 hanno probabilità $\frac 12$ poichè possono essere ottenuti con un lancio con probabilità $\frac 12$ ;i numeri 2, 3, 4 e 5 hanno probabilità $\frac 14$ perchè possono essereottenuti con due lanci con probabilità $\frac 14$ ...

A.- Guarda che la somma delle probabiltà di ciascun evento indipendentedeve essere uguale ad 1 e tu con soli sei numeri hai gia raggiunto il numero2:

$\begin{displaymath}%% P(0)+P(1)+P(2)+P(3)+P(4)+P(5)= %% \end{displaymath}$

$\begin{displaymath}%% =\frac 12+\frac 12+\frac 14+\frac 14+\frac 14+\frac 14=2 %% \end{displaymath}$

B.- Ma basta che poi divida per un fattore di normalizzazione (che in questocaso è 2) ed ottengo

$\begin{displaymath}%% P(2)=P(3)=P(4)=P(5)=\frac 18 %% \end{displaymath}$

A. - La tua idea è buona se vuoi definire la probabilità a priori diuna quantità finita di numeri; ma se vuoi considerare tutti i numeri iltuo fattore di normalizzazione diventa

$\begin{displaymath}%% 2\cdot \frac{1}{2}+4\cdot \frac{1}{4}+8\cdot \frac{1}{8}+.....=1+1+1+.....=%%% \infty %% \end{displaymath}$

A. - Quasi nel modo che hai detto tu. Lanci la tua moneta e la successionedi ''0'' ed ''1'' che ti viene sarà considerata un programma e messa inuna maccina di Turing universale e aspetti il risultato. Questa volta lasomma delle probabilità di ciascun numero ti verrà minore (o al piùuguale) a uno, almeno se tu usi un piccolo accorgimento ovvero che nessunprogramma sia uguale alla parte iniziale di un altro programma. Questocapita molto spesso nei programmi reali. Basta che un programma ''dichiari''in anticipo la sua lunghezza. In questo caso la probabilità a priori di unnumero è definita da

$\begin{displaymath}%% P(n)=\sum_{U(p)=n}2^{-\left\vert p\right\vert } %% \end{displaymath}$

A.- Cerco di spiegartela: la probabilità che la tua moneta produca ilprogramma

è data da $2^{-\left\vert p\right\vert };$ quindi se vuoi definirela pobabilità che il tuo computer produca il numero

devi sommare leprobabilità di tutti i prorammi

che producono

ovvero tutti iprogrammi tali che

$\begin{displaymath}%% \Omega =\sum_{n=0}^{\infty }P(n),%% \end{displaymath}$

B. - Anche perchè, volendo dire tutta la verità, si finisce col parlaredi cose troppo difficili che neppure tu conosci....

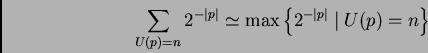
$\begin{displaymath}%% \sum_{U(p)=n}2^{-\left\vert p\right\vert }\simeq \max \left\{ 2^{-\left\vert p\right\vert%% }\mid U(p)=n\right\} %% \end{displaymath}$

B.-E quindi quasi tutti i numeri sono casuali, ma ci sono dei numeri cheavendo leggi nascoste, hanno una maggiore probabiltà di altri di essereprodotti dal ''caso'' e quindi hanno una maggiore probabilità di''esistere''. Ma questa è cabalistica. Pitagora sarebbe stato felicissimoe i maghi del Medioevo avrebbero fatto salti di gioia.

B.- Non ti sto prendendi in giro. Anzi, mi sto divertendo molto. Facciamo unpo' di cabalistica. Prendiamo un numero magico; per esempio il numero diAvogadro. I chimici dicono esso sia

$\begin{displaymath}%% N=6,28\cdot 10^{23}.%% \end{displaymath}$

A.- E' facile ottenere un numero o una stringa casuale, ma è difficiledimostrare che essi sono casuali. In un certo senso si può soltantodimostrare che una stringa non è casuale.

A. - Intuitivamente è molto semplice: una stringa non è casuale se hauna regola nascosta; se tu trovi tale regola, allora essa non è casuale.Se invece non trovi nulla non sai se la tua stringa è casuale oppure sedevi cecare ancora...e ancora...e ancora...e non sai mai quando fermarti.

B.- Ma esisterà certamente un metodo sistematico per stabilire se unastringa è casuale. In fondo, tutti i computer di questo mondo hanno''zippatori''.

A- Ora sei tu che fai uso di brutti neologismi; il nome ''zippatore'' fapiù schifo della parola ''stringa''.

B.- Ma tutti sanno che uno zippatore è un programma che permette dicomprimere un ''file'' e poichè un file non è altro che una stringa, unozippatore mi permette di stabilire se una stringa è casuale o no.

A.- I tuoi zippatori funzionano solo perchè i file che si usano sono benlontani dall'essere casuali.

B. E chi ti dice che io non possa, magari tra 30 anni, inventare lozippatore perfetto.

A.- Me lo dice il teorema di Chaitin. E' un fatto della vita che laperfezione non esiste, e qualche volta questo fatto si può dimostrare ecosì non ci saranno illusi come te che cercano la ''pietra filosofale''.

B.- Allora, se tu vuoi spezzare definitivamente le mie illusioni, spiegamiil teorema di Chaitin.

A.- Parla di numeri e della loro definibilità mediante ''parole''. Peresempio le proposizioni

sono proposizioni che definiscono rispettivamente i numeri 97, 6 e6.915.878.970.

B. Bene fin qui ti seguo. Un tale numero esisterà certamente; infatti datoun qualunque insieme di numeri naturali il minimo esiste sempre.

B.- Certo, altrimenti la matematica sarebbe contraddittoria: ci sonomoltissimi teoremi che derivano dal fatto che un sottoinsieme degli interiha sempre un minimo.

A.- E sei anche sicuro che i numeri descrivibili ''a parole'' formino uninsieme?

A. - Allora supponiamo che tale numero esista e chiamiamolo $\beta$ : ilnumero di Berry. Poichè la proposizione ''@'' contiene 115 simboli(contando anche gli spazi vuoti), ciò vuol dire che per definire $\beta$ ci vogliono almeno 116 simboli.

A.- Ma tu dimentichi una cosa: la proposizione ''@'' contiene 115 simboli edefinisce il numero $\beta .$

B.- Ho detto ''Gasp!'' il che vuol dire ''sono confuso, stupito e noncapisco più nulla''.

A.- Non è proprio il caso che tu ti stupisca tanto; i paradossi e leantinomie in logica come in matematica esistono fino da quando è statoinventato il ragionamento astratto, cioè dai tempi dell'antica Grecia. Ingenere, esse nascono dall'''autoreferenza'', cioè dal disporre di unlinguaggio che può parlare di se stesso.

A.- Sì, più o meno le cose stanno così. Pensa per esempio alparadosso di Epimenide: se uno dice:

$\begin{displaymath}%% \mbox{''io mento'',} %% \end{displaymath}$

B.- Sarà, ma questo numero $\beta$ lo digerisco proprio male. Comunquepenso che queste antinomie sono molto stupefacenti dal punto di vistalogico, ma che sia difficile applicarle a situazioni pratiche come quelleriguardanti computer e programmi. Un programma è un programma: è unacosa concreta che si ''vede'' e non può essere troppo legato alleastrazioni tipo quelle amate dai Greci che nonostante il loro genio teorico,dal punto di vista tecnologico non erano poi un gran che.

A.- Ti sbagli, perchè antinomie e paradossi, opportunamente interpretati,ti dimostrano che certe cose non si possono fare. Stabiliscono le colonned'Ercole che separano il possibile dall'impossibile. Come ad esempio ilparadosso di Berry.

Tradotto nel mondo dei computer, esso diviene un teorema, il teorema diChaitin che stabilisce che con un programma

contenente una quantitàdi informazione

Per ''tradurre'' il paradosso nel teorema occorre spostare l'accento dalcampo dell'esistenza a quello della dimostrabilità. L'espressione ''cherichieda'' deve essere sostituita da ''che si può provare cherichieda''. Inoltre la vaga nozione di ''numero di simboli'' può essererimpiazzata dalla ''informazione algoritmica'' che è una quantitàben definita e misurabile in bit. Usando questi accorgimenti, la ''@''diventa

Se il programma

esistesse, usandolo come subroutine, si potrebbefacilmente costruire il programma @@ che ha una quantità di informazionepoco superiore a quella di

, diciamo

ed opera nel seguente modo:

In altre parole il programma @@ ha prodotto una stringa

che hainformazione algoritmica maggiore di

ovvero

con

$\begin{displaymath}%% I(x)=\min \left\{ \left\vert q\right\vert \mid U(q)=x\right\} \leq \left\vert @@\right\vert%% =k+k_1 %% \end{displaymath}$

Ma mentre il paradosso di Berry ti ha soltanto fatto meravigliare, ilteorema di Chaitin ti insegna anche che non può esistere lo zippatoreperfetto.

B.- Ma allora la tua teoria algoritmica dell'informazione non serve quasi anulla; in pratica non si può mai sapere se una stringa è casuale.Tutt'al più si può solo sapere quello che non si ha speranza di scoprire.

B.- ....a proposito di quello che non si può mai sapere....questi discorsimi fanno venire in mente il teorema di Gödel, quello che dice che inaritmetica ci sono cose vere che non possono essere dimostrate...

A.- Sì, questa teoria ha molto a che vedre col teorema di '' incompletezza'' di Gödel. Chaitin stesso ha dato molte dimostrazioni''informatiche'' di questo teorema.

Ti voglio raccontare in modo un po' intuitivo di cosa si tratta. Torniamoall'aritmetica, alla cabalistica come dici tu.

Prendiamo un numero

e vediamo se ha regole nascoste, ovvero, se pensatocome stringa, esso è comprimibile. Questo fatto non può esseredimostrato con un programma

che ha un contenuto di informazione minoredi

B.- Ma noi, almeno in linea di principio, possiamo prendere programmi lunghiquanto ci pare e alla fine scopriremo se

è o non è un numero casuale.

A.- Certo. Ma ora seguimi un po' in questo ragionamento. Se tu scegli unnumero finito di assiomi e formalizzi tutte le regole di inferenza di unateoria matematica (per esempio l'aritmetica), otterrai un ''programma'' cheha un contenuto di informazione magari grande, ma finito.

B.- Tu vuoi dire che il mio libro di matematica potrebbe essere ridotto adun programma.

C.- Certo. Un programma, chiamiamolo $\mathcal{L}$ , al quale, come input daiun' enunciato, e come output aspetti una risposta: questo enunciato è vero(cioè è un teorema) oppure questo enunciato è falso. Basta che tuformalizzi bene le regole di inferenza, e il tuo programma può produrretutti i teoremi e verificare se essi sono uguali all'enunciato dato, oppuresono uguali alla sua negazione. A questo punto il programma ti da larisposta e si ferma.

Il teorema di Gödel ti dice che un tale programma non può esistere, maquesto fatto te lo dice anche il teorema di Chaitn.

Se la quantità di informazione contenuta in

è maggiore di quella di $%%% \mathcal{L}$ (ossia della quantità di informazione contenuta in assiomi eregole di inferenza) sicuramente, per il teorema di Chaitin, non potrai mairicevere la risposta.

A.- Non ti gasare troppo; in realtà noi abbiamo saltato tutti i dettaglitecnici. Comunque, per me, c'è una cosa ancora più sorprendente: presoun qualunque numero

B.- Questo veramente non è una grande novità, Socrate lo aveva predicatopiù di 2000 anni fa.A.- Già, ma la novità consiste nel fatto che questo vale per sempliciproprietà aritmetiche. Se noi, con un computer potentissimo e con unprogramma

con

A.- Ma non capisci; se questo è vero, viene distrutto il vecchiopregiudizio che la matematica sia un sistema assiomatico deduttivo. Inrealtà essa è una scenza empirica.

A.- La maggior parte delle verità verificate da un semplice modello comel'insieme dei numeri naturali, non possono essere dedotte da un sistemafinito di assiomi, anche se potrebbero essere verificate con altri mezzi;proprio come capita nelle scienze empiriche: una teoria, qualunque essa sia,non ti permette di prevedere tutto. Ci sono sempre fatti che le sfuggono eche richiedono che la teoria venga ampliata. In Aritmetica, quello che èdato a priori è l'insieme dei numeri naturali, ma le veritè che liriguardano, non possono essere dedotte da un insieme finito di assiomi e diregole di inferenza. E quindi l'Aritmetica è una scienza sperimentale.

A.-Un po' sì e un po' no. In realtà, a questo proposito Chaitin haproposto di introdurre la nozione di incerezza in Matematica ed accettareenunciati del tipo:

B.-Adesso capisco perchè mi hai detto che la teoria algoritmicadell'informazione ha conseguenze filosofiche.

A.- No! in realtà quando ho detto questo stavo pensando all'epistemologiadi Salomonoff.

B.- Ma come, non ti basta di aver già tirato in ballo la probabilità,l'informatica, l'aritmetica, la logica e la critica dei fondamenti? Ora tirifuori anche l'epistemologia? E chi è questo signor Salomonoff.

A.- Insieme a Kolmogorov e a Chaitin è il padre di questa teoria. Anzi èil primo ad averne scoperto i punti essenziali. Ma fino a quando Kolmogorovnon li ha riscoperti nessuno ci aveva fatto caso.

Comunque lui è arrivato a questa teoria attraverso altre motivazioni. Eglivoleva trovare un criterio per sapere, almeno virtualmente, quale, tra dueteorie scientifiche fosse la migliore.

Salomonoff ha pensato di rappresentare le osservazioni di uno scienziatomediante una successione di cifre binarie.

A.-Alla teoria spetta il compito di ''spiegare'' le osservazioni e dipredirne delle nuove. Quindi una teoria scientifica può essere consideratacome un programma che permette ad un computer di riprodurre le osservazioni.

B.-E' ovvio, quella più corta, quella capace di zippare maggiormente idati empirici. Tutto questo è molto bello, ma la teoria non è nuova, èla vecchia storia del rasoio di Occam: tra due teorie equivalenti si scegliequella più semplice tagliando via i fronzoli inutili.

A.-Certo che è la vecchia teoria del rasoio di Occam, ma formulatamatematicamente. E questo fatto la fa uscire dalla filosofia delle opinioniper farla approdare ad una epistemologia adatta alla scienza dei nostrigiorni.

B.- Certo questa storia non sarà molto apprezzata da Popper il qualesostiene che il valore conoscitivo di una teoria scientifica si misura dallasua falsificabilità.

Se ci sono due teorie in competizione e se queste teorie sono scentifiche,deve esserci la possibilità di fare un ''esperimento cruciale'' chefalsifichi una delle due e quindi stabilisca quale delle due è ''piùvera''. Se questa possibilità non esiste, non siamo più nel mondo dellascienza ma della metafisica.

A.- Non so cosa pensino i popperiani, ma ti posso dire quello che penso io.A me pare che il criterio di scientificità proposto da Popper siaestremamente riduttivo. Per esempio niente della matematica sarebbe unateoria scientifica; o forse lo sarebbe la geometria Euclidea, in seguito adaccurate misurazioni relative agli enunciati dei suoi teoremi. E non solo lamatematica sarebbe esclusa dal mondo della Scienza, ma anche molte teoriequali la teoria dell'evoluzione naturale, la teoria del big-bang, la teoriadella deriva dei continenti, l'astronomia,...

B.- Forse hai ragione. In fondo la scienza moderna è nata con larivoluzione Copernicana, e Copernico, a fare gli esperimenti, non ci pensavanemmeno. Per lui la teoria eliocentrica era ''vera'' solo perchè zippavale osservazioni fatte dagli astronomi nei 2000 anni precedenti. E ora che cipenso anche Kepler, ha sostituito le ellissi agli epicicli perchè conpochi parametri riusciva a descrivere le posizioni dei pianeti conaltrettanta accuratezza; e se anche teniamo conto delle osservazionisuccessive, aumentando opportunamente il numero degli epicicli si sarebbepotuto descrivere il moto di qualunque pianeta con l'accuratezza desiderata.

A.-Vorresti dire che Kepler è stato il più grande zippatore della NuovaScienza?

B.-Ma anche Galileo non schezava mica..... Ma come la mettiamo con il fattoche non si può sapere quando una stringa è zippabile.

A.- Vuoi dire qual'è il significato epistemologico del teorema di Chaitin?In fondo ci dice quello che il buon senso ci ha sempre detto: non si puòsperare di avere un algoritmo che ci permette di trovare in ogni occasionela teoria ottimale. La scoperta di una buona teoria è frutto di lavoro,intelligenza, intuizione e molta fortuna.

B.- Vuoi dire che il cervello umano con lavoro, intelligenza,intuizione e molta fortuna riesce a fare quello che un computer non riescea fare?

A.- Questo ovviamente non lo sa nessuno. Ma possiamo provare a formularemeglio il problema mediante la tesi di Church.

A.- Church è un signore che è considerato il maggior logico di questosecolo dopo Gödel. Mentre Gödel ha dimostrato che esistono cose vere chenon possono essere dimostrate, Church ha provato che non esiste alcun metodoper sapere se una cosa è dimostrabile.

B.- Per favore cerca di precisare meglio quello che intendi perchè non tisto capendo.

A.- Considera un sistema formale, ovvero un linguaggio, degli assiomi edelle regole di inferenza. Il tutto deve essere perfettamente formalizzato:questo in pratica vuol dire che tutto il lavoro potrebbe essere fatto da uncomputer. Inoltre il nostro sistema formale deve ''contenere'' una teoriaabbastanza ricca: diciamo l'aritmetica. Dandogli tempo infinito, questocomputer dovrebbe essere capace di stampare tutti i teormi.

A. Bene! Gödel ti di dice che certe proposizioni non saranno mai stampate.Nè loro nè le loro negazioni. Dunque, aggiungendoci un po' di fantasiasi può dire che certe cose non sono nè vere, nè false. Questo fatto siesprime dicendo che il sistema è incompleto.

A.- Dice che non esiste una procedura di decisione, ovvero, persapere se una cosa è dimostrabile o no, non ti resta altro che aspettareche il computer stampi quella proposizione o la sua negazione. Fino allafine del tempo. Non c'è alcun metodo generale che ti permetta di sapere apriori quali sono i teoremi dimostrabili. L'unico mezzo a disposizione èquello di provare a dimostrarli, ma se non ci riesci, non puoi dedurrenemmeno che non sei abbastanza bravo.

B.- Però, da come io vedo le cose, mi sembra che sia dal teorema diGödel che dal teorma di Church non si possano trarre troppe conseguenzefilosofiche. Gödel e Church hanno provato che tutti i sistemi formali sonoincompleti e mancano di una procedura di decisione. Ma questo è come direche in geometria Euclidea non si può quadrare il cerchio o trisecarel'angolo. In realtà queste costruzioni sono possibili; basta aggiungerequalche nuovo marchingegno alla riga e al compasso. Analogamente, èpossibile inventare qualche nuovo strumento, per esempio un supercomputerparallelo, oppure, ampliare le regole del gioco per poterne sapere di piùsulle verità aritmetiche. In fondo potrebbe capitare di tutto; chissa comestanno le cose?

A.- In realtà sembra proprio che questo ampliamento non sia possibile;infatti Turing usando la sua macchina ideale, con metodi completamentediversi è giunto proprio alla stessa conclusione. E questo fatto haportato Church a suggerire che qualunque effettiva computazione (odimostrazione) operata da uomini e macchine poteva essere duplicata dall'uomo ideale o dalla macchina ideale e questa è la famosatesi di Church. E' una affermazione empirica, ma l'evidenza a suo favore èschiacciante. Poichè ogni operazione fatta da una macchina ideale o da unuomo ideale può essere fatta da una macchina di Turing universale, la tesidi Church-Turing può essere riformulata così:

''Tutto quello che può essere zippato,può essere zippato da una macchina di Turing''

Ogni computer, anche il più potente non può fare niente di più diciò che può fare una macchina di Turing universale. Ovvero, qualunquealgoritmo può essere simulato da qualunque semplice computer, bastasupporre che abbia memoria infinita e che si abbia la pazienza di aspettare.

B.- Sembra impossibile che quel macinino da caffè possa fare tutti i contie dimostrare tutti i teoremi concepibili. Ma, se le cose stanno così,allora tutto quello che vediamo e facciamo può essere simulato da unamacchina di Turing.

A.- Adesso non esagerare, tu non stai formulando la tesi di Church-Turing,ma la tesi di Church-Turing-Signor B. che recita così:

e francamente mi sembra che sia un po' troppo. In fondo l'universo èpiuttosto grande. Ci sono più cose in cielo e terra di quanto latua filosofia possa sognare. Nel mondo fisico ci possono essere fenomeniche sfuggono ad una descrizione algoritmica. Dando per buona la tesi diChurch, ci si può porre la seguente domanda:

Esiste qualche fenomeno fisico che calcola qualcosa di non-calcolabile?

B.- Ho capito dove vuoi arrivare. Stai semplicemente riformulando la miadomanda: può il cevello umano fare quello che un computer non riesce afare, nemmeno ipoteticamente?

A.- Hai ragione; ormai abbiamo chiacchierato anche troppo. Andiamo al bardella facoltà a farci la solita partita a Magic con il resto dellacompagnia.