A three-manifold M is a list of lines concluded by a line which contains
the string ``-------------------'' only.

The first line contains a single integer n, which means that a geometric triangulation P of M with
n tetrahedra will be given below. The next 2n lines describe P in SnapPea format (see also this
annoted example -courtesy of Jeff Weeks). The tetrahedra of P are labeled by the integers from
0 to n-1, and the vertices of each tetrahedron are labeled by the the integers from 0 to 3.

The next n+1 lines describe the dihedral angles along the edges of the tetrahedra of P.
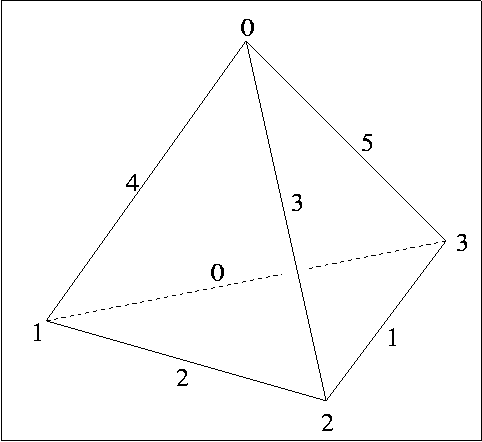
The line labeled ``N. i'' contains the 6 angles of the tetrahedron labeled i.
Edges are labeled from 0 to 5 and angles are listed according to the labels of the edges.
There is no natural labeling rule for the edges, so we have chosen the following arbitrary rule:
 


 
 

The meaning of the subsequent lines is obvious: we indicate the total volume and the volume
of the individual tetrahedra, the boundary (where T^(g) stands for the surface of genus g, which
gives a cusp for g=1 and c component of the boundary for g>1), a presentation of the fundamental
group, and the first homology group.
 
 

Page last updated on May 16, 2014