Lezione 7

Laboratorio didattico di matematica computazionale
Docente: Beatrice Meini

Lezione 7: Figure in R^3

ATTENZIONE: al termine della lezione inviare a meini AT dm.unipi.it i file creati.

Grafici di funzioni RxR ----> R
Vogliamo disegnare il grafico della funzione f (x,y) = 2 sin ( sqrt(x^2 + y^2) ), con (x,y) appartenenti al rettangolo [x1,x2] x [y1,y2]. Per far questo si scriva una function grafico(u,v), che prende in input un vettore u e un vettore v, che "discretizzano" gli intervalli [x1, x2] e [y1, y2], rispettivamente, e che disegna il grafico della funzione, calcolandola nelle coppie ( u(h), v(k) ), dove u(h) e v(k) sono la h-esima e la k-esima componente di u e v, rispettivamente.
Suggerimento: si utilizzino le istruzioni meshgrid e mesh. Si vedano i rispettivi help per il loro uso, oppure il manuale.

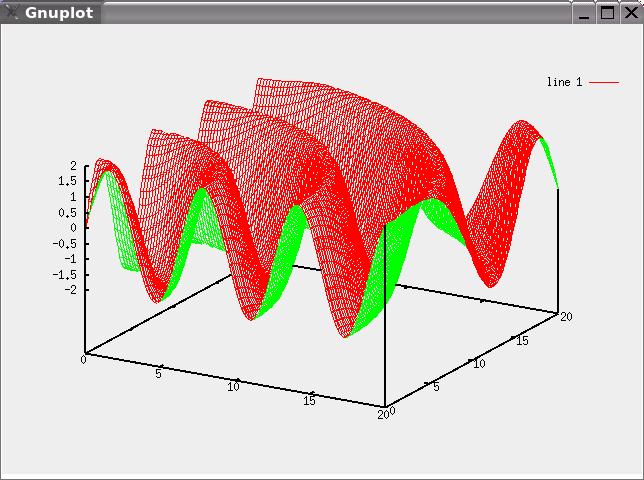
Scegliendo u = v = 0: .2 : 20 dovreste ottenere la figura

grafico

Successivamente:

Modificare a piacere la funzione che si vuole disegnare.
Si disegni il paraboloide ellittico, definito dalla funzione f ( x, y) = (x^2 / 2 + y^2 / 3) /2.
Si disegni il grafico della funzione f( x, y)= x exp( - ( x - y^2 )^2 - y^2 ) in un intorno di (0,0).

Curve nello spazio
Le seguenti equazioni parametrizzano una curva in R^3 di coordinate (x(t), y(t), z(t)):

x(t) =(1+t^2)sin(20 t),
y(t) =(1+t^2)cos(20 t),
z(t) =t, con t in [ -5, 5].

Si scriva una function che disegna la curva. Si utilizzi la funzione gsplot, con l'opzione gset parametric. Per l'uso di veda il manuale. Dovreste ottenere
Modificare la function per ottenere una "molla".
Disegnare le curve:

x(t) =(2+cos(1.5 t)) cos(t), y(t) = (2 + cos(1.5 t)) sin(t), z(t) =2 sin(1.5 t), con t in [ 0, 4 pi].
x(t) =(4+sin(20 t)) cos(t), y(t) = (4 + sin(20 t)) sin(t), z(t) =cos(20 t), con t in [ 0, 2 pi].
x(t)=t, y(t)=t^2, z(t)=t^3, con t in [-2, 2].
x(t) = sin (t), y(t) = sin(2 t), z(t)= sin(3 t), con t in [0, 2 pi].

Disegnare altre curve a piacere.

La striscia di Moebius
La striscia di Moebius è descritta dalle equazioni parametriche

x(u,v) = cos(u) + v cos(u/2) cos(u)
y(u,v) = sin(u) + v cos(u/2) sin(u)
z(u,v) = v sin(u/2),

con (u,v) in [0, 2 pi] x [- 0.4, 0.4]
Scrivere una function moebius che disegna mediante le istruzioni meshgrid e mesh la striscia di Moebius.

Esercizi per casa:

Scrivere:

una function che disegna la sfera di centro 0 e raggio r, dove r viene dato come input
una function che disegna l'ombrello di Whitney, ossia la superficie rappresentata dall'equazione x^2 y = z^2, o equivalentemente dalle equazioni parametriche:
x = u
y = v^2
z = u v (si prendano u in [-2, 2], v in [-2, 2])